Je vais vous montrer une preuve mathématique proprement ahurissante. Nous allons démontrer que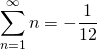. La somme des entiers relatifs tend vers .

Cela devrait vous paraître totalement ahurissant, car à priori , mais c’est pourtant bien le cas.
Mieux encore, ce résultat que l’on pourrait croire purement mathématique se retrouve dans des problèmes physiques très sérieux, dont la théorie des cordes et la théorie quantique des champs.

C’est la preuve la plus simple (et pas extrêmement stricte mathématiquement parlant) que je vous montre ici.

Tout d’abord, prenons notre série 

Multiplions-la par 4 : 

Soustrayons ce résultat à notre série S d’origine, de manière à avoir 

(1)  

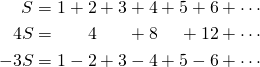
Mais pourquoi aligner mes lignes de cette manière ?

Pour mieux soustraire.
Évidemment, c’est tricher, car on ne fait pas la soustraction terme à terme. Seulement, comme tout va à l’infini, on peut juger que de toute manière, cela se rattrape. Reprenons.
Nous avons à présent l’expression qui est en réalité la série alternée des entiers et dont nous connaissons le résultat grâce à Euler, soit .
Ainsi donc, , soit .
On a donc 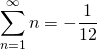. CQFD.

On a donc un résultat plutôt aberrant qui pourrait largement remettre en cause la méthode selon laquelle nous l’avons déterminé. Pourtant, je peux vous affirmer (me croirez-vous ?) qu’il est correct.

Les plus curieux/courageux/fous iront chercher des preuves alternatives du côté des séries de Riemann et de Dirichlet, c’est aussi très sympathique bien que plus dur mais exactement sur le même principe que ce que je viens de montrer.

Ce post de blog (merci Amaury pour me l’avoir fait retrouver) est excellent sur le sujet.

Allez, avant de finir, un dernier clin d’œil bien sympathique :

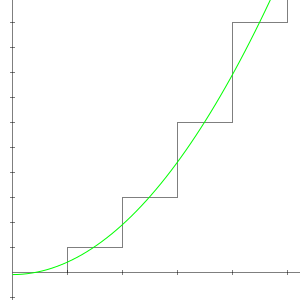
Si on calcule l’asymptote, on se rend compte que l’asymptote en l’origine tend vers . Cool, non ?

Images : Portraits respectivement de Riemann, Euler et Dirichlet, tous les trois dans le domaine public.